Difference between revisions of "Nanoparticle acoustic transducers"
| Line 20: | Line 20: | ||
where each layer is characterised by the size parameter ''x<sub>L</sub>=2πNr<sub>l</sub> /λ'' and the relative refractive index ''m<sub>l</sub>=n<sub>l</sub>/n<sub>m</sub>'', where ''λ'' is the wavelength of the incident wave in vacuum, ''r<sub>l</sub>'' is the outer radius of the lth layer, ''n<sub>m</sub>'' and ''n<sub>l</sub>'' are the refractive index of the medium outside the particle of its lth component, respectively, and ''k'' is the propagation constant. | where each layer is characterised by the size parameter ''x<sub>L</sub>=2πNr<sub>l</sub> /λ'' and the relative refractive index ''m<sub>l</sub>=n<sub>l</sub>/n<sub>m</sub>'', where ''λ'' is the wavelength of the incident wave in vacuum, ''r<sub>l</sub>'' is the outer radius of the lth layer, ''n<sub>m</sub>'' and ''n<sub>l</sub>'' are the refractive index of the medium outside the particle of its lth component, respectively, and ''k'' is the propagation constant. | ||
| + | |||
| + | [[File:Sensitivity gold in air.png|600px|alt=alt text]] | ||
| + | [[File:Sensitivity air polystyrene gold ts20nm.png|600px|alt=alt text]] | ||
==Mechanical modelling== | ==Mechanical modelling== | ||
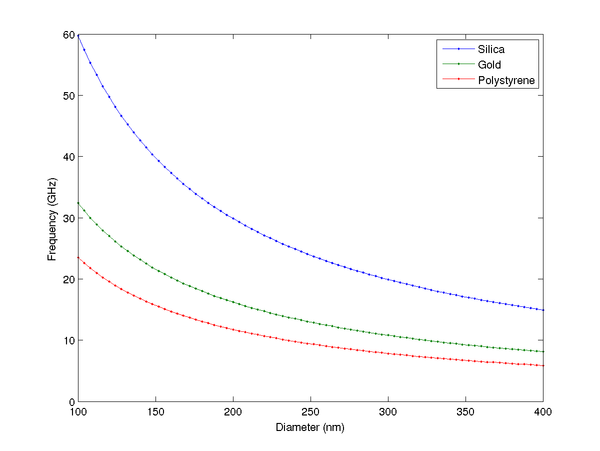
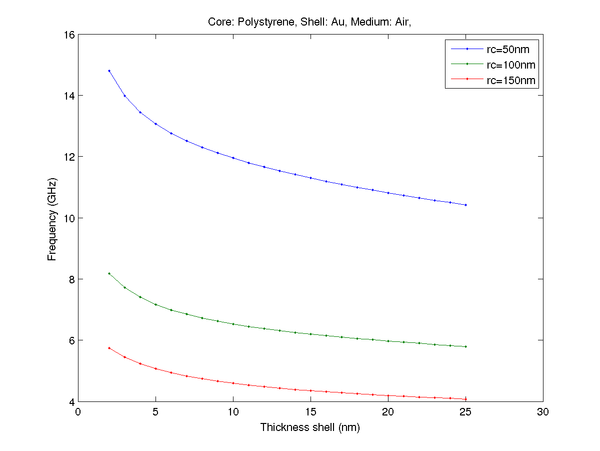
In order to make our transducers resonate at a specific frequency, the main breathing mode frequency has to be modelled based on the parameters of the transducer. The acoustical properties of a nanoparticle in a matrix can be described in terms of vibrations of a homogeneous elastic body embedded in an infinite homogeneous medium. | In order to make our transducers resonate at a specific frequency, the main breathing mode frequency has to be modelled based on the parameters of the transducer. The acoustical properties of a nanoparticle in a matrix can be described in terms of vibrations of a homogeneous elastic body embedded in an infinite homogeneous medium. | ||
| + | |||
| + | [[File:Breathing mode solid particles.png |600px|alt=alt text]] | ||
| + | [[File:Polystyrene Gold Nanoshell Air.png |600px|alt=alt text]] | ||
Revision as of 14:50, 7 March 2016
Introduction
There has been much interest in the optical and mechanical properties of solid and core-shell nanoparticles. Our interest stems from the ability of such devices to interact with ultrasound of very short wavelength allowing the possibility of high resolution acoustic imaging.
There are a number of different fabrication approaches that could be adopted for making nano ultrasonic transducers. Previously, a plate transducer for cell imaging has been developed, but making the lateral dimensions of the transducer smaller than one micron is challenging. An alternative approach to overcome this difficulty and to increase the frequency is to make transducers using nanoparticles.
Nanoparticle acoustic transducers have some attractions:
- Small size
- Can be made in large quantities
- Easy symmetry
- Can exploit plasmonics to enhance the detection sensitivity (for metal particles)
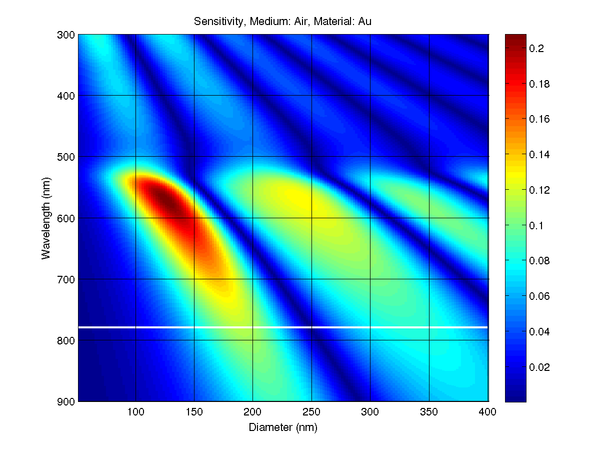
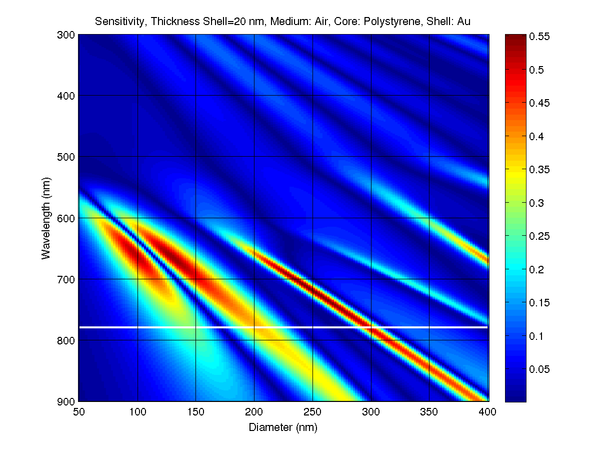
Optical modelling
The optical sensitivity of the transducer is governed by Mie scattering. The layer structure is designed so that the metal layer is partial reflector. Part of the probe beam incident on the transducer is transmitted into the cavity and is resonantly reflected (and transmitted) by the structure. The transducer (when it vibrates) has to show a high optical sensitivity for the probe wavelength (780 nm) in transmission or/and reflection.
The scattering and backscattering efficiencies are obtained:
PICTURE
where each layer is characterised by the size parameter xL=2πNrl /λ and the relative refractive index ml=nl/nm, where λ is the wavelength of the incident wave in vacuum, rl is the outer radius of the lth layer, nm and nl are the refractive index of the medium outside the particle of its lth component, respectively, and k is the propagation constant.
Mechanical modelling
In order to make our transducers resonate at a specific frequency, the main breathing mode frequency has to be modelled based on the parameters of the transducer. The acoustical properties of a nanoparticle in a matrix can be described in terms of vibrations of a homogeneous elastic body embedded in an infinite homogeneous medium.